|
Salah Merad (salah.merad@newcastle.ac.uk)
Rogério de Lemos (r.delemos@newcastle.ac.uk)
Department of Computer Science
University of Newcastle upon Tyne
NE1 7RU, UK
Abstract
We consider the problem of the optimal selection of software components
from a library of components with respect to some non-functional attributes.
Two potential solutions are presented, one based on utility theory, and
the other based on a game theoretic formulation of the problem.
1. Introduction
In this position paper, we consider the problem of selection
from a library of several components which have the same functionality,
but differ in their non-functional attributes (NF-attributes). Examples
of NF-attributes are reliability, performance, availability, which together
specify the quality of service provided by a component, and cost. In the
selection process, a trade-off between cost and quality of service has
to be made.
A similar multi-criteria decision problem was addressed
by Kontio /Kontio 96/ for which he recommended using the Analytic Hierarchy
Process developed by Saaty /Saaty 90/. We propose two solution procedures:
the first one is based on the construction of a combined utility function
that quantifies the user�s preference patterns over the available components,
and the second one is the result of a game theoretic formulation of the
problem. In the latter, a group or subset of components that have the same
functionality is to be selected, and we propose an index which is a measure
of the trade-off between the overall quality of service to be provided
by the group and the total cost of the software to be built. We briefly
discuss the conditions under which each of the solutions is applicable
and the criteria which need to be considered to evaluate the merits of
each solution procedure.
2. Optimal selection of components
Given a user�s non-functional requirements (NF-requirements),
the problem is to select the "best" component or subset of components from
a library of components with respect to their NF-attributes.
2.1. The model
Let 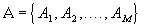 be the set of components which satisfy the user�s requirements. Let
be the set of components which satisfy the user�s requirements. Let  be
be 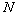 NF-attributes
that specify the quality of a component. Let NF-attributes
that specify the quality of a component. Let 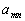 be the level of attribute
be the level of attribute 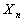 in component
in component 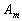 , , 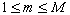 and
and 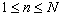 . Then,
vector . Then,
vector 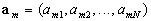 represents the profile of component
represents the profile of component 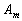 . .
We distinguish two types of NF-requirements, strict
and flexible. Without loss of generality, we define these terms for an
attribute 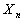 in
which the user�s preference is for high levels over low levels. A NF-requirement
for attribute in
which the user�s preference is for high levels over low levels. A NF-requirement
for attribute 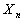 is strict when the level of the attribute in a component has to be equal
or higher than a critical level
is strict when the level of the attribute in a component has to be equal
or higher than a critical level 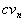 ,
and it is flexible when the level can be lower than ,
and it is flexible when the level can be lower than 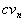 ,
though the user aspires for higher levels. The user�s strength of preferences
over the levels of attribute ,
though the user aspires for higher levels. The user�s strength of preferences
over the levels of attribute 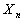 are summarised in a utility function
are summarised in a utility function 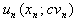 whose expression is found empirically. The user�s NF-requirements are specified
by the vector
whose expression is found empirically. The user�s NF-requirements are specified
by the vector 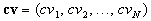 and the individual utility functions
and the individual utility functions 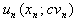 , , 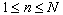 . .
Let 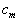 be the cost of component
be the cost of component  ,
and ,
and  the
total amount of money available for expenditure on components. Without
loss of generality, we assume that the
total amount of money available for expenditure on components. Without
loss of generality, we assume that 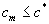 for all
for all  . .
2.2 Solution procedures
This is a multi-attribute decision problem for which
there exists a large literature /Fishburn 70, Keeney 76/. For this problem,
there is no obvious solution concept because there are many attributes,
some of which are conflicting. We consider two solutions: one is an extension
of the Von Neumann one-dimensional utility function to several dimensions,
and the other is the result of a game theoretic formulation of the problem.
2.2.1. Combined utility function
It is shown that, under some independence assumptions
between the attributes, it is possible to represent the user�s preferences
between alternatives with a combined utility function (CUF) 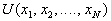 which has a simple expression. For example, under the assumption of preference
independence, in which the user�s preference pattern over a subset of attributes
is independent of the levels of the complementary subset, the CUF has the
additive form
which has a simple expression. For example, under the assumption of preference
independence, in which the user�s preference pattern over a subset of attributes
is independent of the levels of the complementary subset, the CUF has the
additive form
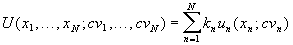 ,
where ,
where 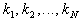 are
scaling coefficients through which the user�s value trade-offs between
the attributes are evaluated empirically. Note that both the individual
utility functions and the CUF are scaled from 0 to 1. The hardest task
is the evaluation of the scaling coefficients which is done through what
are called indifference experiments. We illustrate such experiments with
two attributes are
scaling coefficients through which the user�s value trade-offs between
the attributes are evaluated empirically. Note that both the individual
utility functions and the CUF are scaled from 0 to 1. The hardest task
is the evaluation of the scaling coefficients which is done through what
are called indifference experiments. We illustrate such experiments with
two attributes 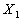 and
and 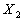 in
which the lowest levels are in
which the lowest levels are 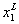 and
and 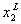 , respectively.
Let , respectively.
Let  be
a possible level for attribute be
a possible level for attribute 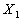 .
The user is then asked to find the level .
The user is then asked to find the level  for attribute
for attribute 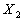 such that he/she is indifferent between the two components which have profiles
such that he/she is indifferent between the two components which have profiles 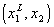 and
and 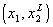 , respectively.
The profiles , respectively.
The profiles 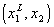 and
and 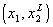 are thus
equivalent and yield the same utility. It is easy to verify that, by combining
the equality of the utilities with the form of the utility function, we
obtain a linear equation. For are thus
equivalent and yield the same utility. It is easy to verify that, by combining
the equality of the utilities with the form of the utility function, we
obtain a linear equation. For 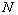 attributes, we need
attributes, we need 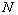 linearly independent equations, and hence at least
linearly independent equations, and hence at least 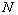 indifference experiments need to be conducted. Because the evaluation process
is subjective, it often yields inconsistencies which are difficult to eliminate
even after repeating the process many times. Note that the cost of components
is one of the attributes, and hence the trade-off between cost and quality
is incorporated in the CUF.
indifference experiments need to be conducted. Because the evaluation process
is subjective, it often yields inconsistencies which are difficult to eliminate
even after repeating the process many times. Note that the cost of components
is one of the attributes, and hence the trade-off between cost and quality
is incorporated in the CUF.
Kontio considered a similar problem and investigated
two solution methods, the Weighted Scoring Method (WSM) and the Analytic
Hierarchy Process (AHP) /Kontio 96/. He recommended the latter method because
it is theoretically sound, it constructs the user�s utility function for
each attribute and it has a strong empirical validation. It is true that
the AHP is superior to the WSM, but it has some shortcomings. The AHP is
a method which yields an additive aggregate utility function which has
the same form as the combined utility function under preference independence
given above. In this aggregate utility function, the scaling coefficients
are replaced by the weightings of the attributes, and the scaled individual
utilities of the CUF are replaced by utilities evaluated by pairwise comparisons
of the alternatives for each attribute separately. These utilities are
in fact weights which add to 1, and which represent ratio scale preferences
between the alternatives. Hence, although the AHP can include the cost
of the components in the aggregate utility, it does not incorporate the
user�s value trade-offs; it is a heuristic which approximates the user�s
true preferences under the preference independence assumption. The AHP
has an advantage in that there are simple statistical tests to check for
consistency in the evaluation of the weighting coefficients and the individual
utilities, but the power of these tests decreases rapidly with the number
of alternatives and attributes.
2.2.2. A game theoretic solution
As mentioned above, the combined utility function requires
the tedious task of the evaluation of scaling coefficients. Moreover, the
NF-requirements for some attributes may be determined by the environment
and hence uncertain (e.g., memory available to run an application at a
given time). For these reasons, we need to define another solution concept
which is appropriate for dealing with the uncertainties associated with
the environment of a component based software system.
Note that although there may be uncertainty regarding
the NF-requirements of some attributes, we assume that the user can quantify
their relative likelihood with a completely specified probability distribution.
In this solution, we assume that, subject to the
user�s purchasing power, a group of different components all fulfilling
the functional requirements is to be selected according to some criterion.
The main issue here is how to evaluate a group of components. To distinguish
between the quality of service provided by a group of components and their
total cost, the cost attribute is not included among the 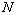 attributes. attributes.
Let 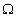 be the set of subsets of
be the set of subsets of 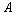 whose total cost does not exceed
whose total cost does not exceed  .
Let .
Let 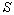 be
an element from be
an element from 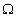 containing the
containing the 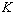 components
components 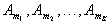 ,
and ,
and  its
cost. Note that its
cost. Note that  can be more than the total of its constituent components, because we need
to add the cost of putting them together.
can be more than the total of its constituent components, because we need
to add the cost of putting them together.
In any subset, there may be more than one component
which satisfies the NF-requirements. If we try to optimise simultaneously
all the attributes, then it can be shown that this selection problem can
be formulated as a bargaining game whose solution achieves a compromise
between the preference patterns of all the attributes /Merad 99/. The solution
is obtained by maximising a function, called the Nash product, over part
of the boundary of a well defined convex set - see /Nash 1950, Luce 57/.
It is a randomised procedure in which the components of the subset are
selected with some probabilities during run-time. The Nash product is
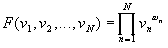 ,
where ,
where 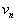 represents
the expected utility for attribute represents
the expected utility for attribute  ,
and ,
and 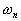 is
the weight allocated to attribute is
the weight allocated to attribute  ,
with ,
with 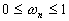 and and 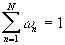 .
These weights are evaluated empirically. .
These weights are evaluated empirically.
Let  be the resulting optimal selection strategy within the subset during run-time
under NF-requirements
be the resulting optimal selection strategy within the subset during run-time
under NF-requirements  .
The elements of vector .
The elements of vector  are
the probabilities with which the respective components are selected. We
propose to characterise the subset are
the probabilities with which the respective components are selected. We
propose to characterise the subset  by the index
by the index
 ,
where ,
where 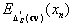 is
the expected level of attribute is
the expected level of attribute  with respect to probability distribution
with respect to probability distribution  . .
If the subset contains only one component, or only
one component in the subset satisfies the NF-requirements, then 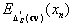 must be replaced by the level of the component for attribute
must be replaced by the level of the component for attribute  .
If no component in the subset is feasible under requirements , then the
index takes value 0. The index under all possible requirements, denoted
by .
If no component in the subset is feasible under requirements , then the
index takes value 0. The index under all possible requirements, denoted
by 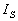 , is
then the average index under all possible requirements, that is , is
then the average index under all possible requirements, that is
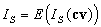 ,
where ,
where 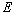 is an expectation with respect to the distributions of the unknown requirements.
If there are no attributes for which the NF-requirements are unknown, then
the index is
is an expectation with respect to the distributions of the unknown requirements.
If there are no attributes for which the NF-requirements are unknown, then
the index is 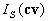 . .
Note that this index is to be computed during the
design phase, and the subset with the highest index in the one that should
be purchased.
Example: Suppose that there are two attributes specifying the
quality of service provided by a component, each of weight 0.5:
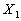 represents
the reliability of a component, and it is measured in average failures
during a given length of time; represents
the reliability of a component, and it is measured in average failures
during a given length of time;
 represents
performance, and it is measured in the time taken to execute a number of
tasks. represents
performance, and it is measured in the time taken to execute a number of
tasks.
The following table gives the profiles of 3 components, together with
the user�s critical values and utilities which appear between brackets
in bold:
| |
Reliability
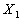
|
Performance
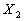
|
|
Critical Values
Components |
1
|
0.8
|
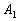 |
0.85
(1)
|
0.80
(0)
|
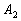 |
0.90
(0.5)
|
0.75
(0.5)
|
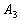 |
0.95
(0)
|
0.70
(1)
|
Consider the two subsets 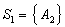 and
and 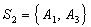 . In
the latter subset, the Nash product is maximised by choosing each of components . In
the latter subset, the Nash product is maximised by choosing each of components 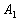 and
and 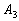 with
probability 0.5 /Merad 99/. The expected level of reliability is 0.9 and
the expected level of performance is 0.75. The indices of the two sunsets
are: with
probability 0.5 /Merad 99/. The expected level of reliability is 0.9 and
the expected level of performance is 0.75. The indices of the two sunsets
are: 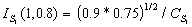 ,
and ,
and  .
If the cost of component .
If the cost of component 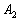 is less than the total cost of subset
is less than the total cost of subset 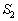 ,
then component ,
then component 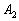 is preferred.
is preferred.
3. Conclusion and future work
We have proposed two solution concepts to the optimal
selection of components under scarce resources, and there are others simpler
but ad-hoc procedures /Merad 99/. The solution concept that should be adopted
depends on the information the user can provide, the practicality of the
computations, especially during run-time, and most importantly the trade-offs
between the computational effort and the gain in utility over simpler but
cruder methods. But the best way of carrying out such an evaluation is
a properly designed experiment in a real situation using real decision
makers /Chankong 83/.
References
/Chankong 83/ V. Chankong and Y.Y. Haines. Multiobjective Decision
Making: Theory and Methodology. North-Holland, 1983.
/Fishburn 70/ P.C. Fishburn. Utility Theory for Decision Making.
Wiley, New York, 1970.
/Keeney 76/ R.L. Keeney and H. Raiffa: Decisions with Multiple Objectives:
Preferences and Value Tradeoffs. Wiley, New York, 1976.
/Kontio 96/ J. Kontio. "A Case Study in Applying a Systematic Method
for COTS Selection". Proceedings of the 18th International
Conference on Software Engineering. Berlin, Germany, March 25-30, 1996.
Los Alamitos, CA: IEEE Computer Society Press, 1996. pp. 201-209.
/Merad 99/ S. Merad, R. de Lemos and T. Anderson. Dynamic Selection
of Software Components in the Face of Changing Requirements. Technical
Report No 664, Department of Computing Science, University of Newcastle,
UK, 1999.
/Nash 50/ J.F. Nash: The Bargaining Game. Econometrica, 18, 1950.
pp. 155-162.
/Saaty 90/ T. L. Saaty. The Analytic Hierarchy Process. McGraw-Hill,
New York, 1990.
/Von Neumann 47/ J. Von Neumann and O. Morgenstern. Theory of Games
and Economic Behavior. Wiley, 2nd edition, 1947.
download the PDF file
contact the organizers
The Software
Engineering Institute (SEI) is a federally funded research and
development center sponsored by the U.S. Department of Defense
and operated by Carnegie Mellon University.
Copyright
2001
by Carnegie Mellon University
URL: http://www.sei.cmu.edu/papers/37/37.htm
Last Modified: 27 September 2000
|
